Module réseaux sociaux

Les graphes

Imaginez un réseau social ayant 6 abonnés (A, B, C, D, E et F) où :

A est ami avec B, C et D
B est ami avec A et D
C est ami avec A, E et D
D est ami avec tous les autres abonnés
E est ami avec C, D et F
F est ami avec E et D

La description de ce réseau social, malgré son faible nombre d'abonnés, est déjà quelque peu rébarbative, alors imaginez cette même description avec un réseau social comportant des millions d'abonnés !

Il existe un moyen plus "visuel" pour représenter ce réseau social : on peut représenter chaque abonné par un cercle (avec le nom de l'abonné situé dans le cercle) et chaque relation "X est ami avec Y" par un segment de droite reliant X et Y ("X est ami avec Y" et "Y est ami avec X" étant représenté par le même segment de droite).

Voici ce que cela donne avec le réseau social décrit ci-dessus :

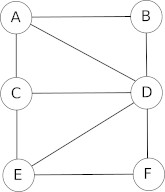
Ce genre de figure s'appelle un graphe. Les graphes sont des objets mathématiques très utilisés, notamment en informatique. Les cercles sont appelés des sommets et les segments de droites des arêtes.

Activité 9.1

Construisez un graphe de réseau social à partir des informations suivantes :

A est ami avec B et E
B est ami avec A et C
C est ami avec B,F et D
D est ami avec C,F et E
E est ami avec A,D et F
F est ami avec C, D et E

Voici quelques définitions sur les graphes :

chaîne : Dans un graphe, une chaîne reliant un sommet x à un sommet y est définie par une suite finie d'arêtes consécutives, reliant x à y.

exemple : Dans le graphe donné ci-dessus, A-D-E-C est une chaîne

distance entre 2 sommets : La distance entre deux sommets d'un graphe est le nombre minimum d'arêtes d'une chaîne allant de l'un à l'autre.

exemple : dans le graphe ci-dessus, la distance entre le sommet A et le sommet F est de 2 (chaîne A-D-F). ATTENTION : on parle bien du nombre minimum d'arêtes, A-D-E-F est aussi une chaîne entre A et F mais dans ce cas, nous avons 3 arêtes.

excentricité : L'excentricité d'un sommet est la distance maximale existant entre ce sommet et les autres sommets du graphe.

exemple 1 : Toujours dans le graphe ci_dessus : distance (A-B) = 1 ; distance (A-C) = 1 ; distance (A-D) = 1 ; distance (A-E) = 2 ; distance (A-F) = 2 ; nous pouvons donc dire que la distance maximale existant entre le sommet A et les autres sommets du graphe est de 2 (distance (A-E) et distance (A-F)). Nous pouvons donc dire que l'excentricité de A est de 2.

exemple 2 : distance (D-A) = 1 ; distance (D-B) = 1 ; distance (D-C) = 1 ; distance (D-E) = 1 ; distance (D-F) = 1 ; nous pouvons donc dire que l'excentricité de D est de 1.

centre : On appelle centre d'un graphe, le sommet d'excentricité minimale (le centre n'est pas nécessairement unique).

exemple : Dans le graphe ci-dessus tous les sommets ont une excentricité de 2 à l'exception du sommet D qui a une excentricité de 1, nous pouvons donc affirmer que le centre du graphe 1 est le sommet D

rayon : On appelle rayon d'un graphe G, l'excentricité d'un centre de G.

exemple : D a une excentricité de 1, c'est le centre du graphe 1, nous pouvons donc dire que le rayon du graphe ci-dessus est de 1.

diamètre : On appelle diamètre d'un graphe G, la distance maximale entre deux sommets du graphe G.

exemple : Dans le graphe ci-dessus la distance maximale entre 2 sommets est de 2, nous pouvons donc dire que le diamètre du graphe est de 2.

Activité 9.2

Soit le graphe suivant (graphe 2) :

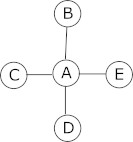
Déterminez le (ou les) centre(s) du graphe 2, en déduire le rayon du graphe 2. Déterminez le diamètre du graphe 2.

Activité 9.3

Soit le graphe suivant (graphe 3) :

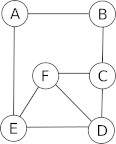
Déterminez le (ou les) centre(s) du graphe 3, en déduire le rayon du graphe 3. Déterminez le diamètre du graphe 3.